I have updated the plots with the data up to May 24, 2020, and highlighted Wisconsin since people seem to be interested in what’s happening there.
While I haven’t lived in Michigan in 27 years, I still have many friends and family members that live there, and I go there fairly regularly. It seems many people are upset with how their governor has handled the shutdown and enforced social distancing, although it appears from polls that the majority of people support her policies.
Besides simply being upset that small business owners are being hurt by this, it seems that many people are upset that they were/are not allowed to go to vacation properties that are usually located in rural areas of northern Michigan. I suspect the thought here was that this was part of an overall limiting of travel. I can understand this from a health perspective as it would keep the spread in areas where there are far more healthcare resources. I can also understand that at a time when people are social distancing, they would like to be able to get away for a bit, and in many ways increase social distancing.
I have also heard many complaints about not being able to go out in boats, and I have to say I really do not understand the reasoning for this. Maybe it’s to limit the number of people that need to monitor boating and/or needing to respond to emergencies. While boating isn’t a huge thing in Pennsylvania, I don’t think there are any limitations here, and I’ve not heard of this in other states; but I may be wrong.
Finally, it seems people are particularly concerned with barbershops and salons. I’m not sure what the particular concern is with these places other than that many are indeed small businesses. However, there are all kinds of other small businesses that are also being hurt. I can understand the government’s stance to keep them closed to enforce social distancing which is hard to do when you’re getting your hair cut. If we’d have built up our testing capabilities faster, then maybe barbers and beauticians could be regularly tested and given some certificate to ensure customers of this. It also seems like barbers and beauticians have made very public statements about their feelings. However, it seems to me that there are just as many small gym owners and personal trainers as there are barbers and beauticians. I don’t hear about them complaining, although I’m sure they are, at least privately.
So, let’s take a look at the data (with all the caveats attached) for Michigan. First, let’s look at the ratio of day-to-day changes in the number of infected; this is often called R. The plot below shows this for all states with four highlighted for comparison. The points above 1.45 at the start that aren’t highlighted are from Missouri. It’s clear that things started off in Michigan with the virus spreading very fast, and there’s plenty of speculation on why that was.
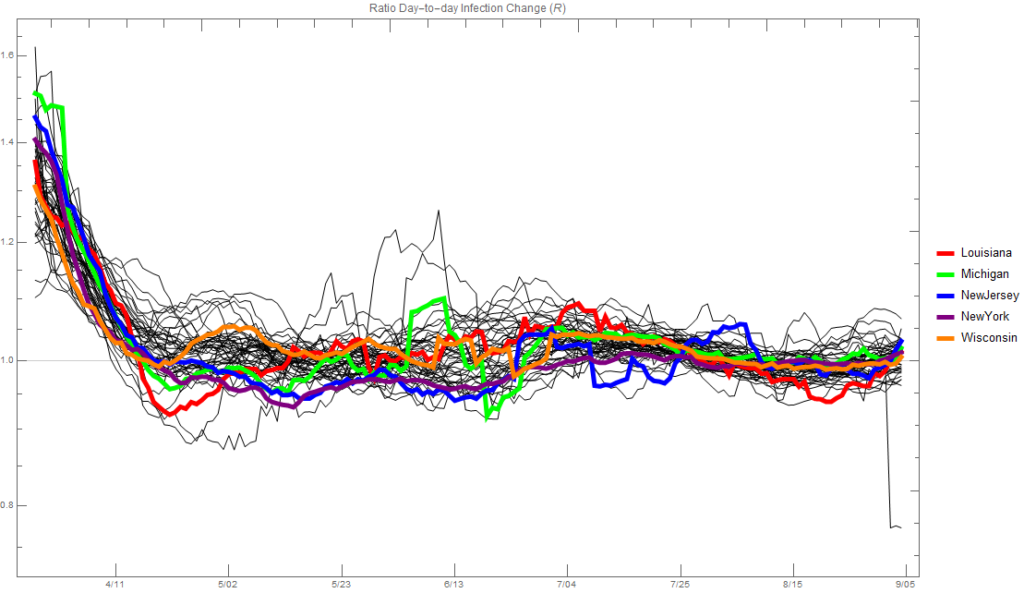
If we look at the new infections each day averaged over a week, we see that, as suggested by the plot above, the infections spread in Michigan very fast. Sometime in the first half of April things changed dramatically, as they did in Louisiana. New infections have now steadied for both states. Note that Michigan’s population is about twice that of Louisiana’s and slightly more than New Jersey’s. Although the infection rate seems to be increasing slightly in the last couple weeks, I suspect the attitude is from a healthcare perspective, “Whatever we’re doing is working, so let’s keep doing it.” From an economic perspective it’s really hard to say, but it’s certainly realistic to think that there could be another explosion in the number of cases. If there is one I suspect it’d be less severe than the first time because people are simply more away and taking precautions. Illinois now has the most new infections of any state, and California is catching up to New York.
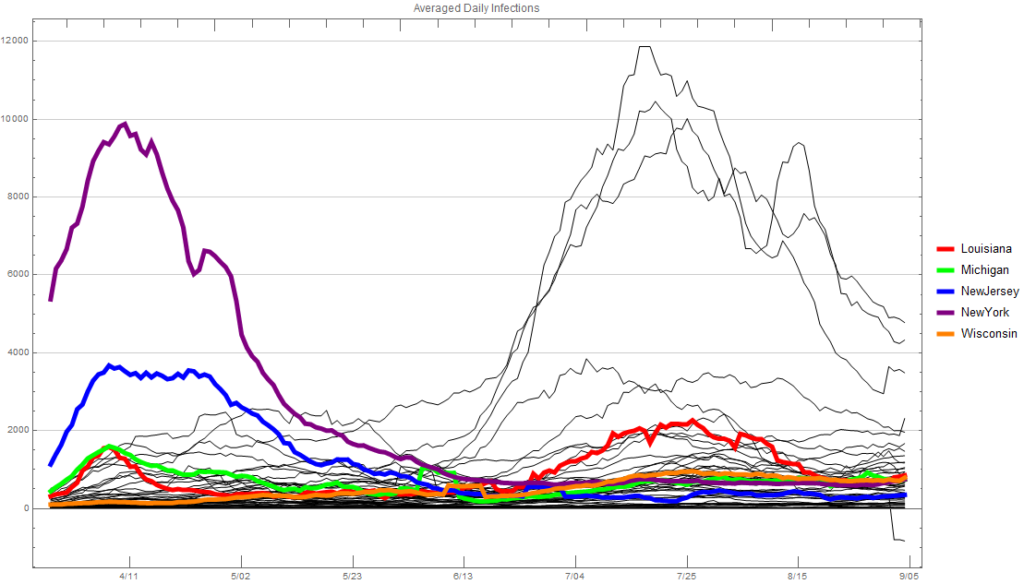
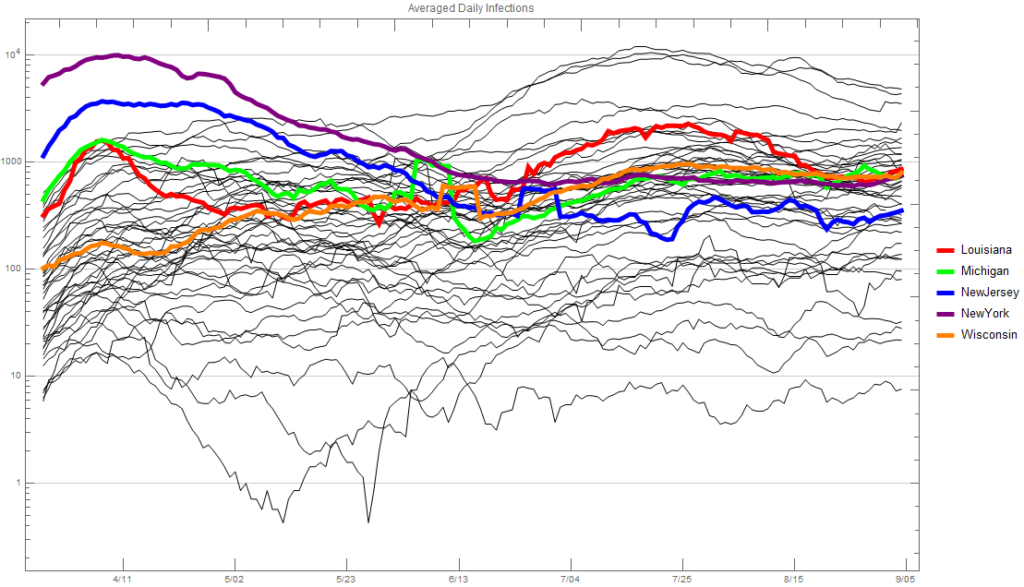
Now let’s take a look at deaths each day, again average over a seven day period. I think this is the one that got the Michigan government/governor very concerned. While the number of daily new infections mirrored that of Louisiana closely, the number of deaths each day was more than double for many days. It’s hard to determine why this was besides maybe an older and less healthy population. Louisiana’s infections were concentrated around New Orleans like Michigan’s were concentrated around Detroit. I doubt the medical care in the Detroit area is any better or worse than in the New Orleans area. Likewise I would think that per capita the capacity would likely be the same.
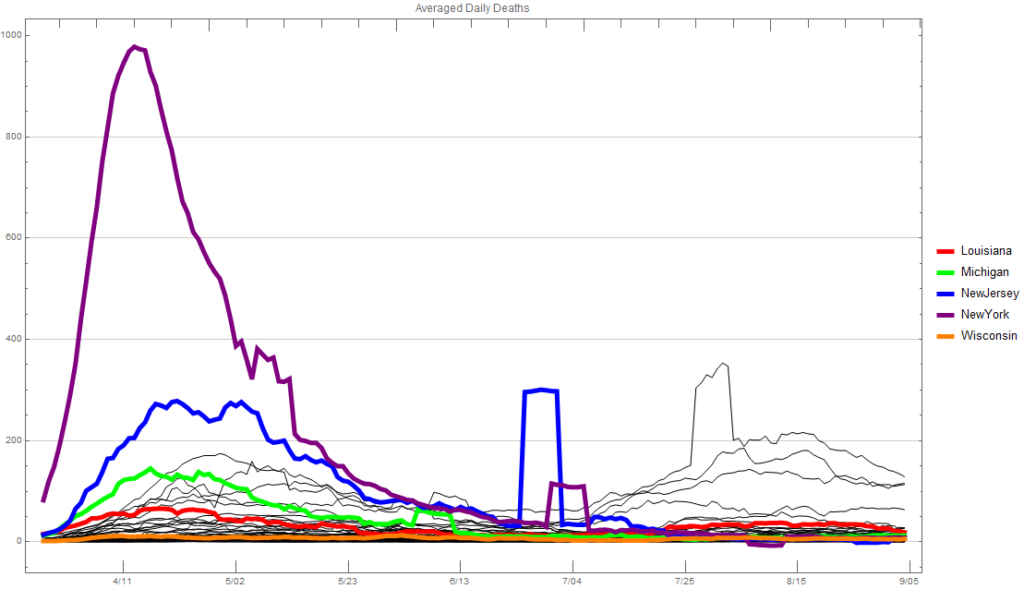
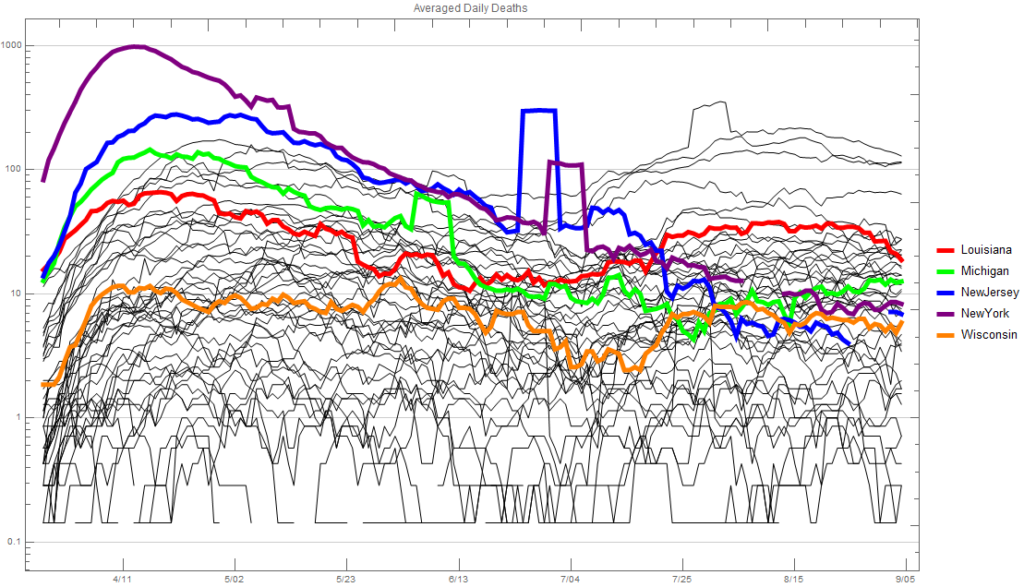
I have no idea if the actions Michigan’s governor took and is taking are the best strategy overall. It certainly seems to be from a healthcare perspective. The big questions that will never be answered are: How many people would have died or gotten severely ill without the actions taken? And, how much better would the economy be without those actions? My personal feeling is that a couple thousand more people would have died and the economy would probably not be a whole lot better. New data from Politico says that “…that Georgia now leads the country in terms of the proportion of its workforce applying for unemployment assistance. A staggering 40.3 percent of the state’s workers — two out of every five — has filed for unemployment insurance payments since the coronavirus pandemic led to widespread shutdowns in mid-March, a POLITICO review of Labor Department data shows.”
I’m not really sure of a good way to look at the life versus economy tradeoff. Maybe the best way is to think that we (you) saved 2,000 lives but lost 2,000 small businesses. That’s still a hard one to judge, but I would think many small business owners would trade their business for the life of a loved one.


You must be logged in to post a comment.